In this note, I provide a MATLAB implementation of finite volume method for solving 1d advection equation. Specifically, it is implementing the Lax-Wendroff scheme with MC limiter from LeVeque (Finite Volume Methods), Section 9.5.2 and onwards. This code assumes that the PDE is conservative, which means
\[\partial_t f + \partial_x(u(x)f) = 0\]and is solved with a padding of ng ghost cells on either side of the mesh boundaries. For stability, temporal integration needs the time step to satisfy CFL condition.
function ff = laxWen1d(f, f_ind, nx, v, dx, dt)
% Takes one time step of 1d conservative advection equation
% via lax-wendroff with MC limiter
% Reference: LeVeque, Randall J. Finite volume methods for hyperbolic problems.
% Vol. 31. Cambridge university press, 2002.
% Input:
% f := solution at current times step, (nx+2*ng,1) vector
% f_ind := indices of f of non-ghost cells
% nx := number of non-ghost cells
% v := variable advec. coeff., (nx+1,1) vector
% defined on left cell edges (1-1/2):(nx+1/2)
% dt and dx are time and spatial step
% Output:
% f0 := (nx,1) solution at next time step on non-ghost cells
% Positive and negative speeds
indp = find(v>0); indm = find(v<0);
vp = zeros(nx+1,1); vm = vp;
vp(indp) = v(indp); vm(indm) = v(indm);
% 1st-order right and left going flux differences
% LeVeque sect. 9.5.2 The conservative equation
% At cell i: Apdq(i-1/2) = right going flux = F(i) - F(i-1/2),
% Amdq(i+1/2) = left going flux = F(i+1/2) - F(i),
% where F is numerical flux.
% Upwind edge flux: F(i-1/2) = vp(i-1/2)f(i-1) + vm(i-1/2)f(i),
% F(i-1/2) = vp(i-1/2)f(i-1) + vm(i-1/2)f(i).
% Apdq(i-1/2)= F(i) - F(i-1/2), Amdq(i+1/2) = F(i+1/2) - F(i);
% F(i-1/2) = vp(i-1/2)f(i-1) + vm(i-1/2)f(i)
% F(i+1/2) = vp(i+1/2)f(i) + vm(i+1/2)f(i+1)
% F(i)
Flux_i = 0;
% F(i-1/2)
Flux_m = vp(1:nx).*f(f_ind-1) + vm(1:nx).*f(f_ind);
% F(i+1/2)
Flux_p = vp(2:nx+1).*f(f_ind) + vm(2:nx+1).*f(f_ind+1);
% Apdq(i-1/2) and Amdq(i+1/2)
Apdq = Flux_i - Flux_m; Amdq = Flux_p - Flux_i;
% W = wave with speed u; p = i+1/2, m = i-1/2
Wp = f(f_ind+1) - f(f_ind); Wm = f(f_ind) - f(f_ind-1);
% theta's for limiter: LeVeque book sect. 9.13
% theta_i-1/2 = q(I) - q(I-1) / Wm , I = i-1 v_i-1/2>=0, =i+1 v_i-1/2<0
% theta_i+1/2 = q(I+1) - q(I) / Wp , I = i-1 v_i+1/2>=0, =i+1 v_i+1/2<0
% Allocate for limiters
Thm = zeros(nx,1); Thp = Thm;
% At i-1/2
xsm = indm(indm<nx+1); xsp = indp(indp<nx+1);
Thm(xsm) = (f(f_ind(xsm)+1) - f(f_ind(xsm)))./Wm(xsm); % negative speed
Thm(xsp) = (f(f_ind(xsp)-1) - f(f_ind(xsp)-2))./Wm(xsp); % positive speed
% At i+1/2
xsm = indm(indm>1)-1; xsp = indp(indp>1)-1;
Thp(xsm) = (f(f_ind(xsm)+2) - f(f_ind(xsm)+1))./Wp(xsm); % negative speed
Thp(xsp) = (f(f_ind(xsp)) - f(f_ind(xsp)-1))./Wp(xsp); % positive speed
% MC limiter: LeVeque sect. 6.12 TVD Limiters eqn (6.39a)
phip = max(0,min(min((1+Thp)/2,2),2*Thp));
phim = max(0,min(min((1+Thm)/2,2),2*Thm));
% mW = modified wave, LeVeque sect. 9.13 eqn (9.69)
mWp = phip.*Wp; mWm = phim.*Wm;
% 2nd-order limited corrections: LeVeque sect. 6.15 eqn (6.60)
Fp = 0.5*abs(v(2:nx+1)).*(1 - (dt/dx)*abs(v(2:nx+1))).*mWp;
Fm = 0.5*abs(v(1:nx)).*(1 - (dt/dx)*abs(v(1:nx))).*mWm;
ff = f(f_ind) - (dt/dx)*(Apdq + Amdq + Fp - Fm);
end
If you save the above code to a file, you can run the following experiments
% testing advection with u(x) = x - x^3
% define parameters
% final time
ttf = 1;
% grid size
dy = 0.01;
% spatial grid
yg = (-3:dy:3)';
% number of ghost cells
ng = 2;
% number of effective grid points
ny = length(yg) - 2*ng;
% indexer
idy_f = (ng+1):(ny+ng);
y = yg(idy_f);
% cell centers
ye = [y - dy/2; y(end) + dy/2];
uu = ye - ye.^3;
% refined time step for CFL
dtt = dx/max(abs(uu));
ntt = ceil(ttf/dtt) + 1;
tt = linspace(0, ttf, ntt);
dtt = ttf/(ntt-1);
f = zeros(ny, ntt);
% initial condition
f(:,1) = 3*exp(-0.5*(3*y).^2)/sqrt(2*pi);
for ii = 2:ntt
tmp = [zeros(ng,1); f(:, ii-1); zeros(ng,1)];
% take one step
f(:,ii) = laxWen1d(tmp, idy_f, ny, uu, dy, dtt);
end
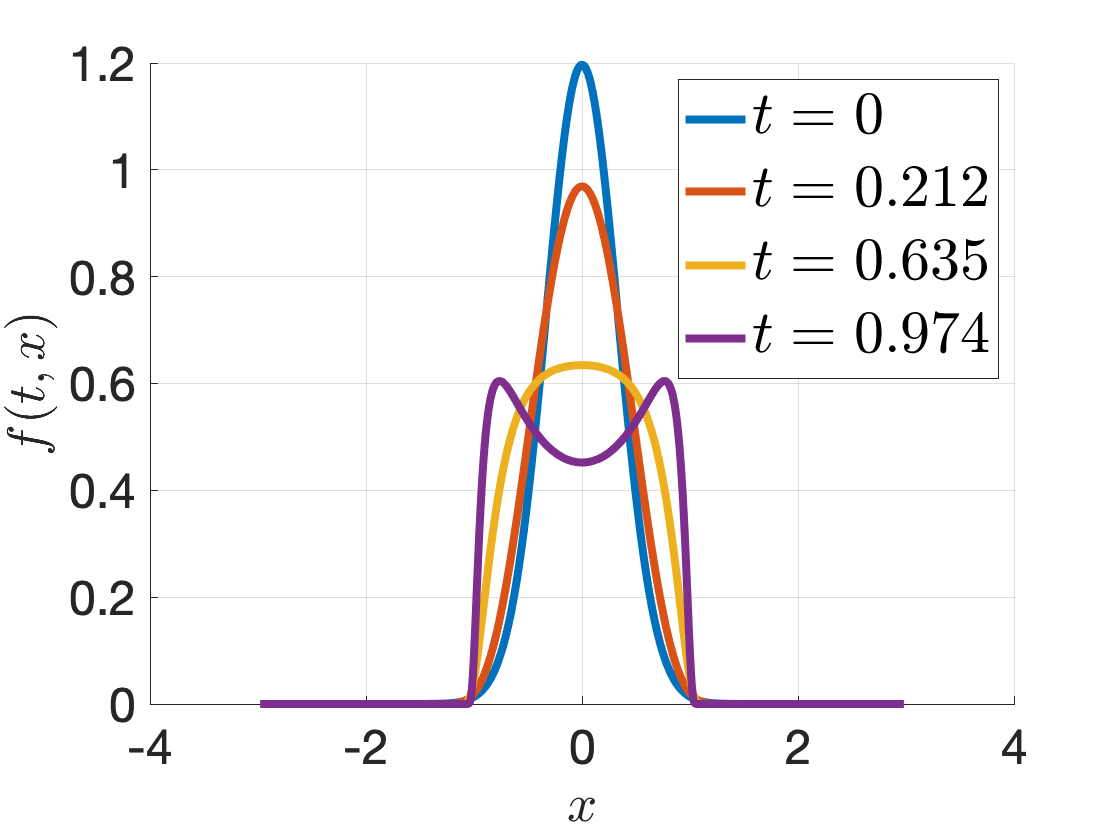
You should expect to see the following solutions:
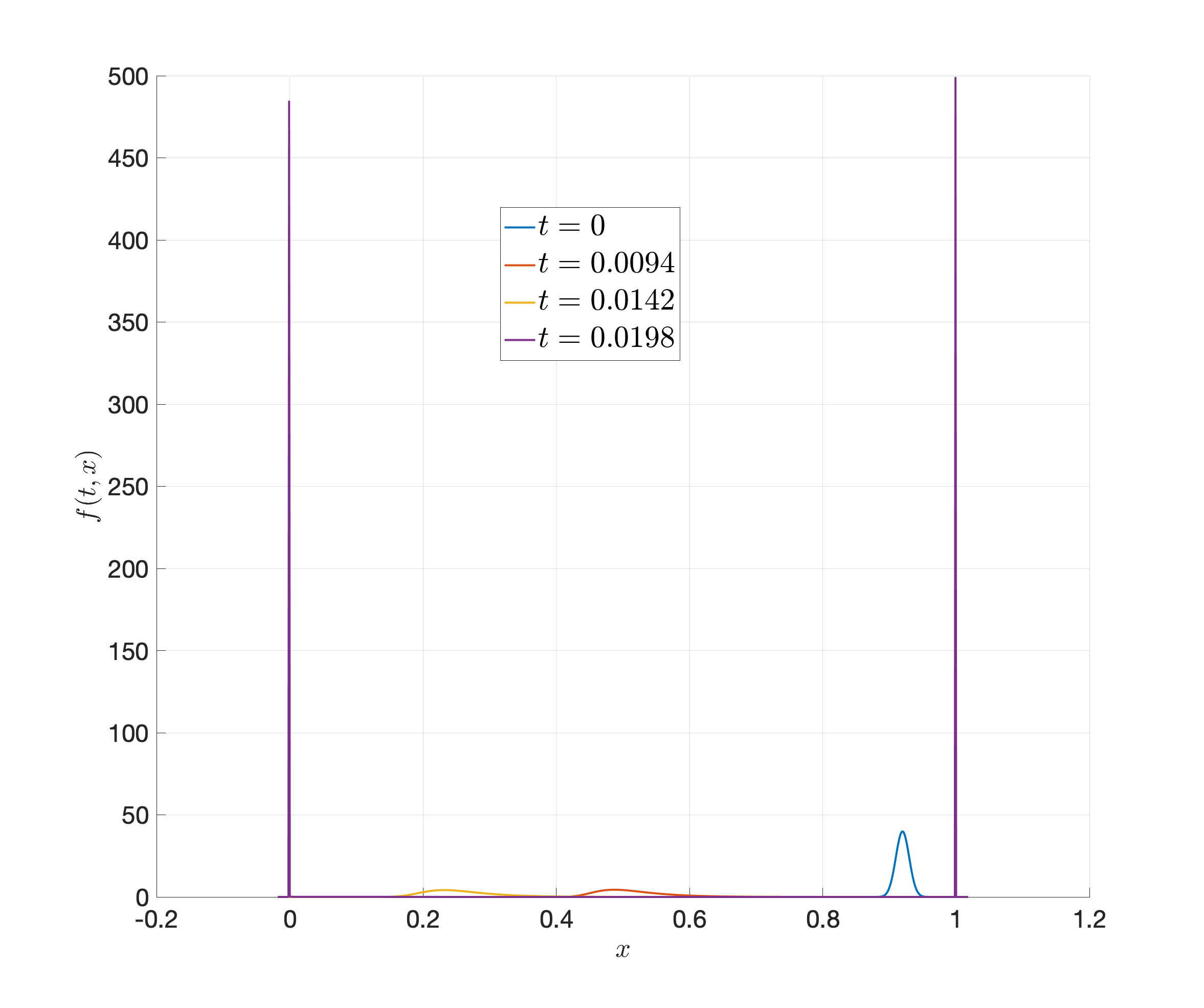
There is another more interesting example where the solution is approximating a fast-changing switch (continuous approximation to indicator). This PDE is very stiff, with \(\Delta t < 10^{-7}\). We provide the code and solutions below.
ttf = .02;
dy = 0.001;
yg = (-0.02:dy:1.02)';
ng = 2;
ny = length(yg) - 2*ng;
idy_f = (ng+1):(ny+ng);
y = yg(idy_f);
ye = [y - dy/2; y(end) + dy/2];
R = 0.0135; D = 1e-4;
uu = 2*R*(-exp(-20*ye) + exp(-200*ye) + exp(20*(ye - 1))...
- exp(200*(ye - 1)) - 0.2 ) / D;
dtt = dy/max(abs(uu));
ntt = ceil(ttf/dtt) + 1;
tt = linspace(0, ttf, ntt);
dtt = ttf/(ntt-1);
f = zeros(ny, ntt);
f(:,1) = 1e2*exp(-0.5*(1e2*(y-.9195)).^2)/sqrt(2*pi);
%f(:,1) = 1/(ye(end) - ye(1));
for ii = 2:ntt
if mod(ii,10000)==0
disp(ii)
end
tmp = [zeros(ng,1); f(:, ii-1); zeros(ng,1)];
f(:,ii) = laxWen1d(tmp, idy_f, ny, uu, dy, dtt);
end