Doodling in Code
This is a twin post of “Doodling Math” where I organize random (pun) code snippets. Typically they are code that solve some probability problems. I like to use Python most of the time; you may find trace amounts of Julia.
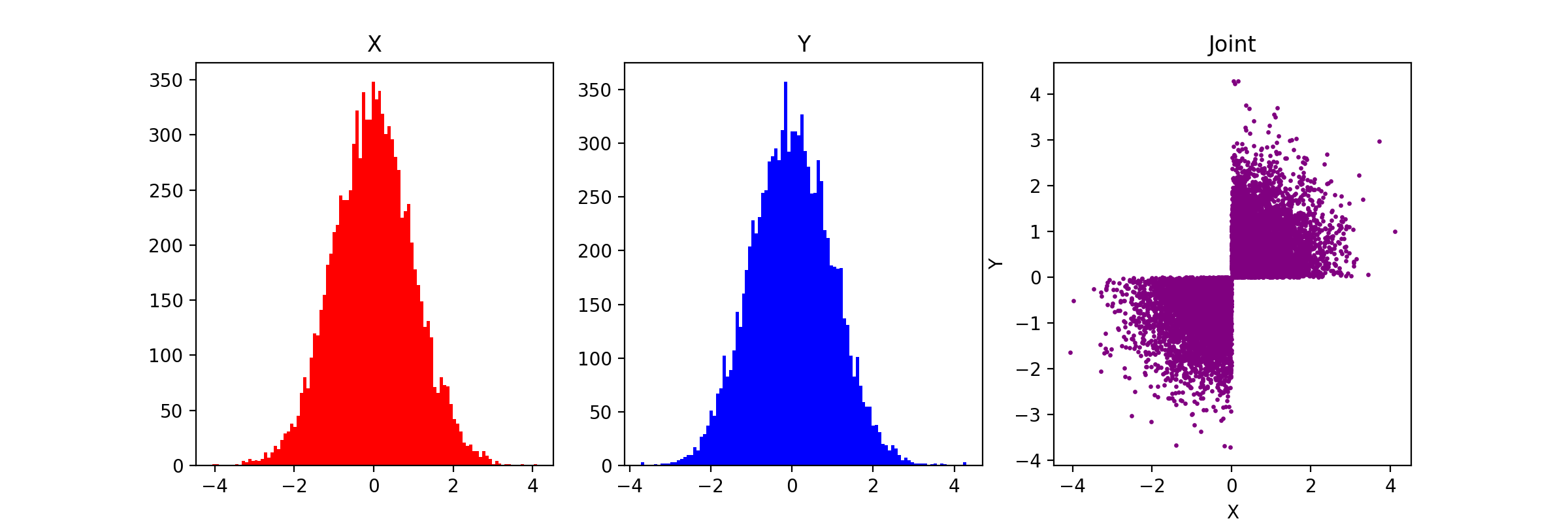
Counterexample of Joint Gaussian Distribution
Two random variables being marginally Gaussian does not imply they are jointly Gaussian. Joint Gaussianity of a random vector \(\mathbf{X}\in\mathbb{R}^d\) means any linear combination of the components is Gaussian. The following is a counterexample: Let \(X, Z\sim \mathcal{N}(0,1)\). Define: \(Y = \begin{cases} Z, XZ\ge 0 \\ -Z, XZ\lt 0 \end{cases}\)
nmc = 10000
x = np.random.randn(nmc)
z = np.random.randn(nmc)
idx = x*z > 0
idx2 = x*z <= 0
y = np.zeros(nmc)
y[idx] = z[idx]
y[idx2] = -z[idx2]
plt.figure(1)
fig, ax = plt.subplots(1, 3, figsize=(20, 4))
nbins = 100
ax[0].hist(x, nbins, color="red"); ax[0].set_title("X")
ax[1].hist(y, nbins, color="blue"); ax[1].set_title("Y")
ax[2].scatter(x, y, color="purple", s=2.0); ax[2].set_title("Joint")
ax[2].set_xlabel("X"); ax[2].set_ylabel("Y")
The plot confirms that they are not jointly Gaussian despite being marginally Gaussian.
Good Old Gambler’s ruin & Black-Scholes
Gambler’s Ruin describes the inevitable loss a gambler faces when playing a game with fixed odds and finite resources. This concept is usually related to using a tree approach for pricing options under different scenarios of underlying.
Designing a class to process a data stream
In the code below, I play with data structures, mainly heaps and deques to achieve \(O(1)\) query of statistics from a data stream: max (or min), avearge, mode (most frequent item, with tie-breaking using the most recently processed point), and median. The maximum, mode and median seem to be non-trivial problems to implement efficiently, especially when one only intends to track \(O(k)\) most recent data.
from collections import defaultdict, deque
import heapq
class DataStream:
def __init__(self, k):
"""
Initialize a data stream object that maintains the max, average, mode, and median for
the k most recent elements.
:param k: size of the window for the sliding window statistics.
"""
self.k = k # Window size (k most recent data points)
self.data = deque() # Deque to store the sliding window of data
self.sum = 0 # Sum to maintain the average
self.max_data = deque() # Deque to store the maximum values in the current window
self.mode_tracker = SlidingWindowModeDeque(k) # Tracker for the mode
self.median_tracker = SlidingWindowMedian(k) # Tracker for the median
def push(self, x):
"""
Add a new element to the data stream and update the statistics.
:param x: new element to add to the stream.
"""
if len(self.data) == self.k:
# If the window is full, remove the oldest element
old = self.data.popleft()
# Update the sum for average calculation
self.sum -= old
# If the old element was the max, update the max deque
if self.max_data[0] == old:
self.max_data.popleft()
# Add the new element
self.data.append(x)
# Update the sum
self.sum += x
# Update the max deque
while self.max_data and self.max_data[-1] < x:
self.max_data.pop()
self.max_data.append(x)
# Update the mode tracker
self.mode_tracker.add_number(x)
# Update the median tracker
self.median_tracker.push(x)
def get_average(self):
"""
Return the average of the k most recent data points.
:return: the average of the sliding window, rounded to 2 decimal places.
"""
return round(self.sum / len(self.data), 2)
def get_max(self):
"""
Return the maximum value of the k most recent data points.
:return: the maximum value in the sliding window, rounded to 2 decimal places.
"""
return round(self.max_data[0], 2)
def get_mode(self):
"""
Return the mode (most frequent element) in the k most recent data points.
:return: the mode of the sliding window.
"""
return self.mode_tracker.get_mode()
def get_median(self):
"""
Return the median of the k most recent data points.
:return: the median of the sliding window.
"""
return round(self.median_tracker.get_median(), 2)
class SlidingWindowModeDeque:
def __init__(self, k):
self.k = k # Size of the sliding window
self.window = deque() # Deque to hold the sliding window elements
self.freq = defaultdict(int) # Frequency map for elements in the window
self.mode_deque = deque() # Deque to track the mode candidates
def add_number(self, num):
if len(self.window) == self.k:
old = self.window.popleft()
# If old was the mode, update
if self.mode_deque and self.mode_deque[0] == old:
self.mode_deque.popleft()
# Update frequency
if self.freq[old] > 0:
self.freq[old] -= 1
if self.freq[old] == 0:
del self.freq[old]
self.window.append(num) # Add new element to the sliding window
self.freq[num] += 1 # Update its frequency
# Maintain the deque in descending order of frequency
while self.mode_deque and self.freq[self.mode_deque[-1]] <= self.freq[num]:
self.mode_deque.pop()
self.mode_deque.append(num)
def get_mode(self):
# The current mode is the element at the front of the deque
return self.mode_deque[0]
class SlidingWindowMedian:
def __init__(self, k):
"""
Initialize the SlidingWindowMedian with window size k.
"""
self.k = k
self.max_heap = [] # Max heap for the smaller half of numbers
self.min_heap = [] # Min heap for the larger half of numbers
self.to_remove = defaultdict(int) # Tracks numbers to remove when they fall out of the window
self.current_size = 0 # Tracks the number of elements in the window
def _balance_heaps(self):
"""
Balance the two heaps so that the sizes differ by at most 1.
"""
if len(self.max_heap) > len(self.min_heap) + 1:
heapq.heappush(self.min_heap, -heapq.heappop(self.max_heap))
elif len(self.min_heap) > len(self.max_heap):
heapq.heappush(self.max_heap, -heapq.heappop(self.min_heap))
def _clean_heap(self, heap):
"""
Clean up the heap by removing any numbers that should no longer be there.
"""
while heap and self.to_remove[heap[0]]:
num = heapq.heappop(heap)
self.to_remove[num] -= 1
def push(self, num):
"""
Add a new number to the sliding window.
"""
if not self.max_heap or num <= -self.max_heap[0]:
heapq.heappush(self.max_heap, -num)
else:
heapq.heappush(self.min_heap, num)
self.current_size += 1
if self.current_size > self.k:
self.pop()
self._balance_heaps()
def pop(self):
"""
Remove the oldest element in the sliding window.
"""
# Remove the oldest element
oldest = -self.max_heap[0] if self.max_heap and (-self.max_heap[0] <= self.min_heap[0]) else self.min_heap[0]
self.to_remove[oldest] += 1
if oldest <= -self.max_heap[0]:
self._clean_heap(self.max_heap)
else:
self._clean_heap(self.min_heap)
self.current_size -= 1
self._balance_heaps()
def get_median(self):
"""
Get the current median of the sliding window.
"""
self._clean_heap(self.max_heap)
self._clean_heap(self.min_heap)
if len(self.max_heap) > len(self.min_heap):
return -self.max_heap[0]
else:
return (-self.max_heap[0] + self.min_heap[0]) / 2
# Example usage and testing
data_stream = [1, 2, 3, 3, 2, -1, 2]
k = 3
track = DataStream(k=3)
for val in data_stream:
track.push(val)
print(f"Window: {list(track.data)}, Average: {track.get_average()}, Max: {track.get_max()}, Mode: {track.get_mode()}, Median: {track.get_median()}")
Brainteaser: Shoelaces
There is a silly problem on stackexchange of connecting shoelaces (some call it spaghetti) into loops and counting how many loops you have, by randomly picking ends of the shoelaces (if you picked two different shoelaces, they merge into one). The brainteaser is asking for the expected number of loops (when you uniformly sample the shoelaces’ ends). The problem can be solved analytically and also simulated. The following is the code.
- Code:
def theo(n):
res = 0
for i in range(1, n+1):
res = res + (1 / (2 * i - 1))
return res
print(theo(100))
import numpy as np
def simulate_outer(n):
memo = {}
def simulate(n):
""" Generates a stochastic output in n noodles. """
if n == 1:
return 1
if n in memo:
return memo[n]
# generate a probability
a = np.random.uniform()
if a <= 1/(2*n-1):
# formed a loop
return 1 + simulate(n-1)
else:
return simulate(n-1)
return simulate(n)
n = 100
nmc = 10000
print(sum([simulate_outer(100) for _ in range(nmc)])/nmc)
import numpy as np
def simulate_noodles(n):
"""Simulate the number of loops formed by randomly connecting n noodles."""
# ends -> noodle
ends = {i: None for i in range(2*n)}
# assign noodles
for i in range(n):
# (the other end, which noodle)
ends[2*i] = (2*i+1, i)
ends[2*i+1] = (2*i, i)
loops = 0
k = n
while k > 0:
left, right = np.random.choice(list(ends.keys()), 2, replace=False)
# if belong to the same noodle
if ends[left][1] == ends[right][1]:
loops = loops + 1
ends.pop(left)
ends.pop(right)
# if does not belong to the same noodle, combine into one
else:
other_end1, noodle1 = ends.pop(left)
other_end2, noodle2 = ends.pop(right)
ends[other_end1] = (other_end2, noodle1)
k = k - 1
return loops
n = 100
nmc = 10000
print(sum([simulate_outer(100) for _ in range(nmc)])/nmc)
They should all give something close to 3.284.
What is a “Trie”?
For fun, let us implement a classic data structure that supports string prefix search and insertion (in linear time). Wikipedia does an execellent job for an introduction.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
def TrieNode():
""" A node in the Trie, contains a list of children. """
self.links = {}
self.end = False
def Trie():
"""
A Trie data structure that can achieve:
=> O(n): insertion
=> O(n): search
=> O(n*k): space, where k is constant, the number of
strings stored in the Trie.
"""
def __init__(self):
self.root = TrieNode()
def insert(self, word):
"""
Adds a word into the Trie.
"""
r = self.root
for ch in word:
if ch not in r.links:
r.links[ch] = TrieNode()
# keep inserting other characters
r = r.links[ch]
# mark end of word
r.end = True
def search(self, word):
"""
Returns a boolean signifying whether `word` exists
in the Trie.
"""
r = self.root
for ch in word:
if ch not in r.links:
return False
else:
# traverse down the Trie
r = r.links[ch]
# check if word ended
return r.end
def prefix(self, p):
"""
Check if a string in the Trie exists with prefix
`p`.
"""
r = self.root
for ch in p:
if ch not in r.links:
return False
r = r.links[ch]
# unlike `search()`, no need to check word ended.
return True
def lcp(self):
"""
Returns the longest common prefix of all words
currently stored in the trie.
"""
res = ""
r = self.root
while r:
# if more than 1 link, means they do not share a
# common char, break
if len(r.links) > 1 or r.end:
return res
ch = list(r.links.keys())[0]
res += ch
r = r.links[ch]
return res
“trie” it yourself by copying the above code and testing on some words.
# input
words = ["hello", "hell", "helloworld", "helium"]
t = Trie()
for word in words:
t.insert(word)
print(t.lcp()) # should return 'hel'
Enjoy Reading This Article?
Here are some more articles you might like to read next: